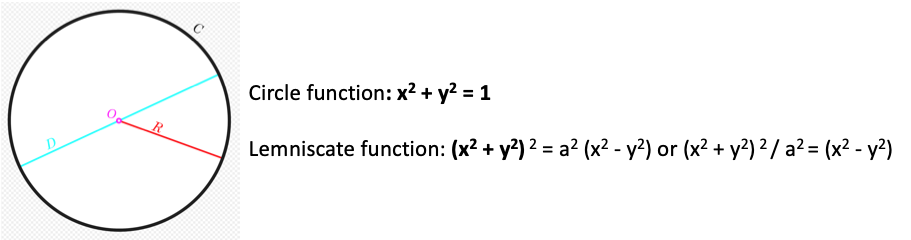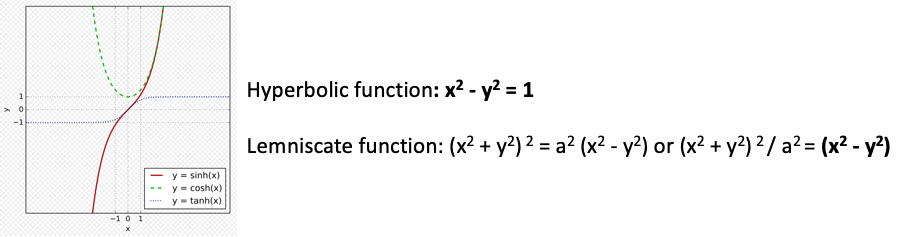Peter Zumthor, the lemniscate, Part 2. While one finds many free-standing architectural masterpieces that utilize a single geometrical shape, few buildings have had an impact on me more than Peter Zumthor’s (1943-) Caplutta Sogn Benedetg near Sumvtig, Switzerland (1985-1988). The chapel, its siting and usage of materials, and the all-encompassing interior space are pure poetry.
Four questions
I was always intrigued by the nature of the chapel’s plan and its association with the curved shape called the lemniscate. Academic research papers and trade journals explore Zumthor’s design process, the project’s history, its materiality, and, occasionally mention the particularity of the design of its cylindrical shape. Yet, I did not find an in-depth explanation of the lemniscate in relation to his work: its origins as a mathematical and geometrical shape, how to draw it, and, most importantly the revelation that I discovered when studying his project. As mentioned in a previous blog about the chapel, I was committed to understanding its shape, and decided to embark on a discovery for answers to the following questions:
What is the nature of this form, which looks like a leaf?
How might one approach the question of representation of this geometry?
To what extent can this form be associated with a circle, a hyperbolic curve,
or an ellipse?
To what extent does this geometry depend on historical precedence?
The Lemniscate
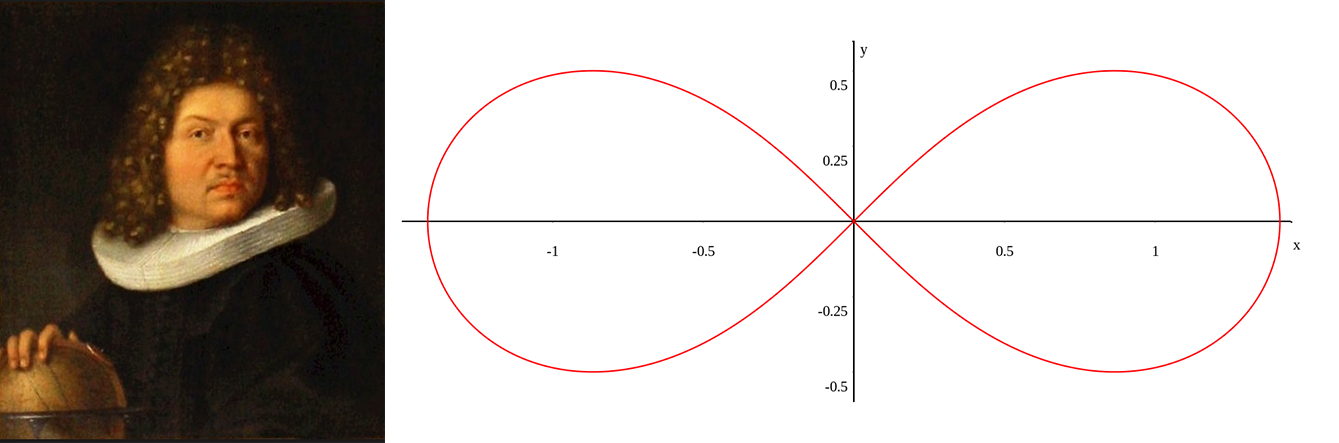
The use of the word lemniscate appears for the first time at the end of the 17th century and is commonly associated with the work of Swiss mathematician Jacob I Bernoulli (1654-1705). Bernoulli belonged to a family of mathematicians who, driven from their Antwerp home during the Catholic persecution of the Huguenots in 1583, settled in the city of Basel; the most northern German speaking city of Switzerland. Basel became one of the chief centers of humanism and the cradle of the Reformation in Switzerland.
In 1694, Bernoulli published an article in the Acta Eruditorum on a curve shaped like a figure eight, a knot, or ribbon bow, for which he used the Latin work lemniscus (‘a pendent ribbon, fastened to a victor’s garland’) thus contributing to the mathematical definition of the curve named lemniscate (Image 1, above). While his main interest in this particular curve remained analytical, through his investigations Bernoulli laid the foundations of the later work on elliptic functions. The characteristics of the lemniscate can be described through its mathematical function and its geometrical figure which are presented below:Image 1: Google images: Jacob Bernoulli and lemniscate (Fig.1)
Mathematical definition
The lemniscate is a figure-eight shaped curve “consisting of all points in the plan such that the product of their distances from two given points, called the foci of the lemniscate, is constant. It is symmetric about the coordinate origin.”
Cartesian equation of the lemniscate:
(x2 + y2) 2 = a2 (x2 – y2) or (x2 + y2) 2 / a2 = (x2 – y2)
x and y are variables and a is a constant equal to the radius of the circle
Polar equation of the lemniscate on the x axis:
r2 = a2 cos (2U) on the X axis
The origin and the genesis of this curve can be found in most textbooks under the chapters of mathematical sine functions, therefore we will not further describe this curve in terms of its mathematical construct. It is important, however, to note that the equation of the lemniscate reveals ‘fragments’ of three equations suggesting its correlation to specific curves, namely the circle, the hyperbole, and the ellipse. Similar to an open book, where words and sentences refer to outside meaning, the lemniscate’s equation gives a series of clues that shed light on its complexity as it belongs to a family of three “unique” curves. With this in mind, a closer examination of the equation of the lemniscate can, to certain degree of transparency, identify three uncompleted functions.
Circular function
First, the CIRCULAR function whose equation is x2 + y2 = 1 is suggested to the left side of Bernoulli’s equation (Image 2, above)
Hyperbolic function
Second, the HYPERBOLIC function whose equation is x2 – y2 = 1 is implicit on the right-hand side (Image 3, above)
Elliptical function
And finally, one can find an indication of the ELLIPTICAL function whose equation is x2/a2 + y2/b2 = 1 (Image 4, above))
The elliptical function is revealed by dividing Bernoulli’s equation by a, which is the radius of the circle, and replacing the constant a in the fraction y2/a2 with the constant b suggesting that there exist two circles with distinct radii a and b. In other words, the equation of the lemniscate and its relationship to an ellipse when a and b are different and to a circle when a and b are equal.
While the discovery of ellipses and their geometrical construction can be traced as far back as 350 BC through the work of Greek geometers and mathematicians, the geometrical principles were revived in the 17th century and rapidly incorporated for architectural purposes in treatises such as Sebastiano Serlio’s The Five Books of Architecture. Yet, it is through Bernoulli’s research on understanding the lemniscate that the mathematical component of the elliptical functions will be developed in the 18th century.
Geometrical interpretation
Teaching architecture and, particularly a second-year design studio, I emphasize that while drawings may be measured and produced mathematically, architects sketch and favor drawing their projects geometrically. However, in a digital world where sophisticated software programs produce “consistent, coordinated, and complete model-based building designs and documentation,” the art of constructing an architectural drawing may seem for many students a bygone era; one that they may have never been exposed to in their freshman year.
In my current institution, we continue to emphasize drawing, sketching, diagraming and conceptualizing, thus I was eager to research and understand how to draw geometrically half of a lemniscate (one single figure-eight curve). For this purpose, I proceeded as follows:
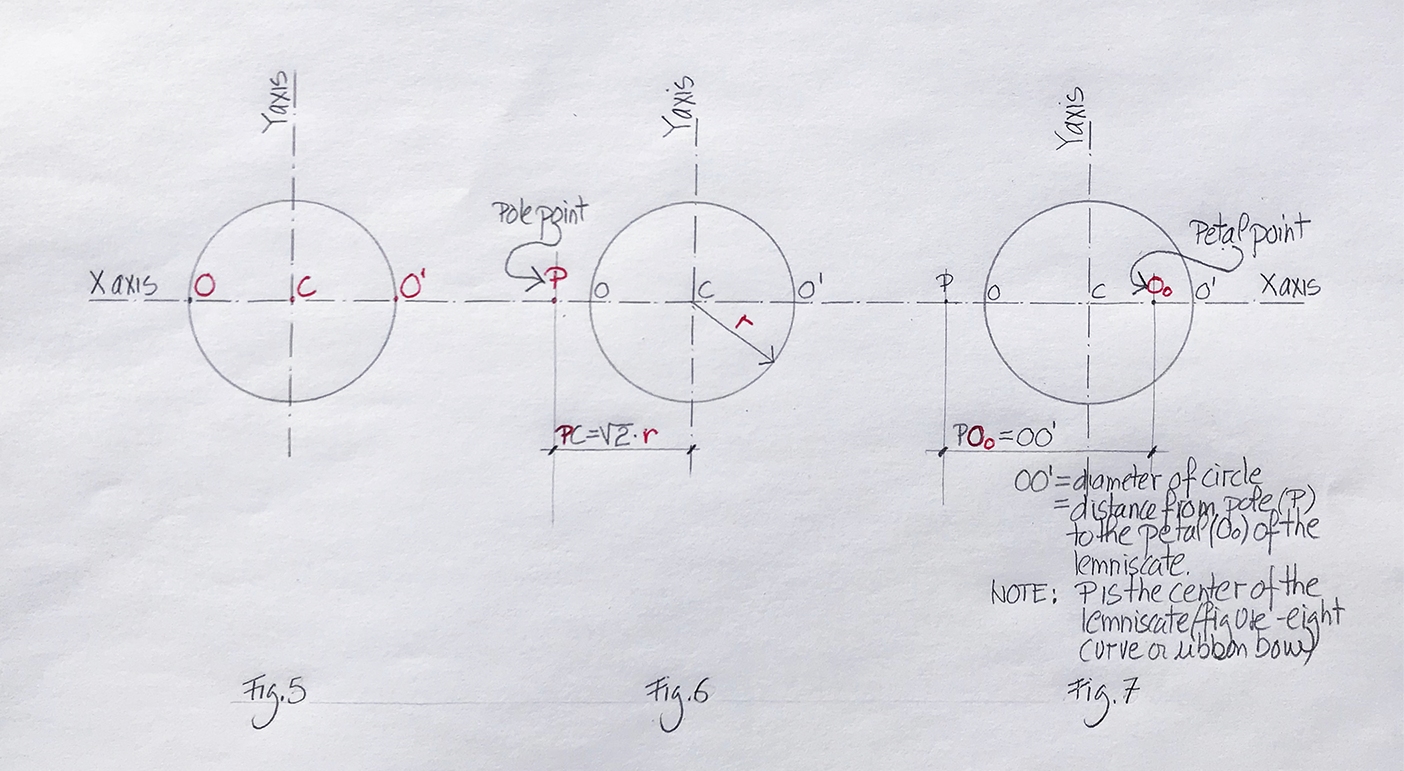
Image 5: (Fig. 1, Fig. 2, and Fig .3) Author’s collection.
How to draw the pole point and the petal point
- (Fig. 1) Draw a circle of any radius and mark the center C. Draw a horizontal line through C corresponding to the X axis, and locate points O and O’ on the circle.
- (Fig. 2) Situate a point P (to the left or right of the circle, it is called the pole point) whose distance from C is √2 times the radius (r). In the above image, P is defined to the left of the circle.
- (Fig. 3) Mark a new point O0 (which will be inside the circle and called the petal point of the lemniscate), which is equal to the dimension OO’ (the diameter of the circle) from point P on the X axis. PO0 constitutes the two furthest points of the lemniscate: the pole point and the petal point.
How to draw the lemniscate, version 1
Image 6: In the description below, I am referring to the highlighted red line (P, R2,O2, S2) shown in the above drawing (author’s collection).
Through P draw any straight line (not parallel to the X axis) that cuts the circle. On this line mark point R2 and S2 where it intersects with the circle. Measure the distance between those two points, and mark the same distance beginning from point P on the same line (PS2). The distance from point P will establish a new point O2. This will constitute one of the many points defining the shape of the lemniscate.
Repeat the process as many times as necessary (15 is a suggested minimum) to create a number of points above and below the X axis (O3, O4, O5…Ox). Then join all those points to form half of the figure-eight curve. The resulting shape will form the basis for Zumthor’s Caplutta Sogn Benedetg Chapel.
Prior to working directly on Zumthor’s plan (Fig. 11 below), I had constructed two additional drawings (Image 7 and 8, below) based on a variable point P on the X axis.
How to draw a lemniscate, version 2

Image 7: Lemniscate where P equals diameter of the circle Author’s collection.
The drawing above (Fig. 7), describes a lemniscate where the point P equals the diameter of the circle (PO0 = OO’), but where PO = OC, which is the radius of the circle. Comparing this drawing with Fig. 7, I noticed that the resulting shape of the lemniscate was flattened.
How to draw a lemniscate, version 3
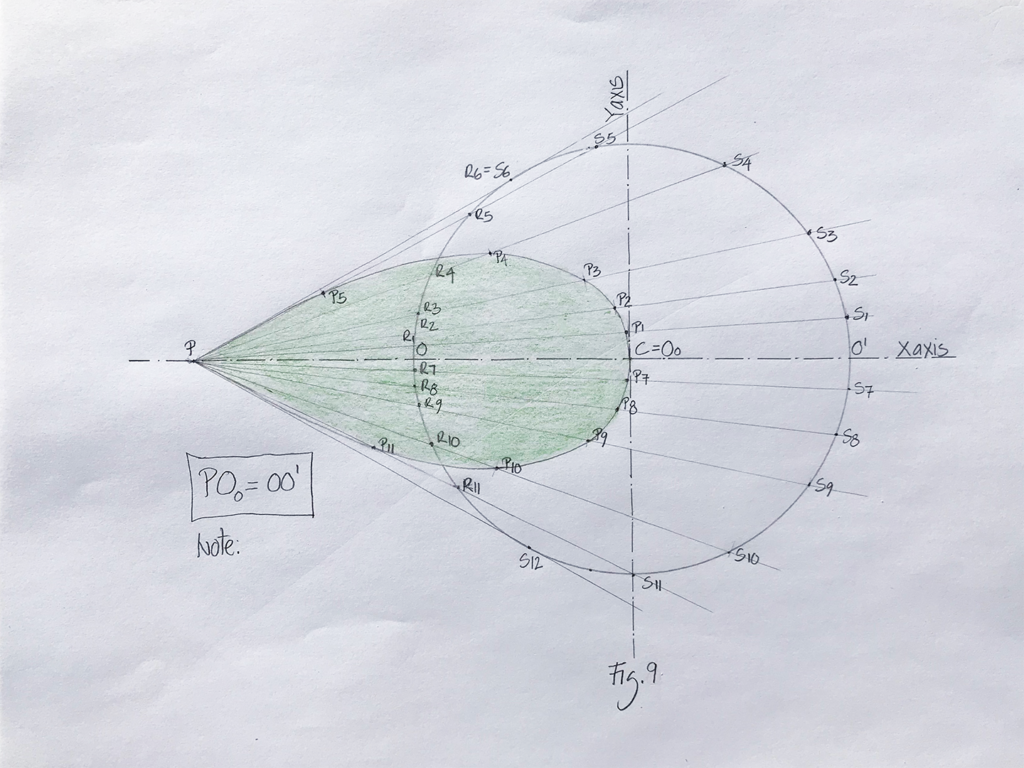
Image 8: A second drawing, shows my choice of an arbitrary point P that is farther away from the circle, and which describes an even flatter lemniscate. Now that I had drawn three different shapes for the lemniscate—two of them, Fig. 7 and Fig. 8, which altered the positioning of P—I was eager to find out how far Zumthor’s lemniscate deviated from Bernoulli’s lemniscate. This assumption was based on Fig. 9 and the actual plan of the chapel. (Author’s collection).
The Plan as translation
Based on the above two drawings (Fig. 6, 7, and 8), the question remaining was to find the size of the circle from which Zumthor’s plan originated, and, more importantly, the circle’s correct position in relation to the lemniscate, as the chapel’s plan (Fig. 11) deviates from the shape of the lemniscate that I had learned to construct (Fig. 8).

Image 9: Lemniscate of Zumthor overlapped with Bernoulli’s lemniscate (author’s collection).
I was fortunate to have purchased two decades ago an edition of Peter Zumthor’s book Häuser, which features a beautiful rendition of the chapel, a precise plan that reflected half of a lemniscate. From constructing Bernoulli’s lemniscate, I knew that PO0 (distance between the pole and the petal points of the lemniscate) equaled the diameter of the circle, thus I needed to find (OO’ highlighted in blue). I divided PO0 by two to get the radius of the circle (r).
Then, using the same mathematical formula (√2 times the radius (r)), I located point O’, which is one of the two points of the circle on the X axis. This was achieved by multiplying AO0 by √2 whose distance I reported from A to locate point O’. From point (O’) I reported the radius of the circle PO0 / 2 to find the center of the circle C. From there, I proceeded to draw the lemniscate according to the method used in Image 6.
Conclusion
Having completed this last step to construct the lemniscate, I was surprised to see that the curve (done according to Bernoulli’s method and which I call ‘first order’ was larger in the y dimension than Zumthor’s curve of the chapel’s plan. Any line drawn perpendicular to the x axis which intersects both curves at two points (Bernoulli’s and Zumthor’s lemniscates) reveal Zumthor’s introduction of a proportional factor of reduction when compared to Bernoulli’s lemniscate, which I then calculated to be equal to ¾. Bernoulli’s equation is thus modified by a factor of reduction ( λ) as follows to achieve Zumthor’s plan:
(x2 + λy2) 2 = a2 (x2 – λy2) where λ is a constant of ¾
This brief history of Bernoulli’s lemniscate and of Zumthor’s geometrical interpretation is of interest to this analysis only insofar as it provides a skeleton for further research on understanding the chapel both in plan and in section. One may speculate as to why Zumthor used a proportional system. In all of my research, I have not found any mention of how he chose the lemniscate, any indication of how to construct this curve, or the need to introduce a proportional system to flatten Bernoulli’s lemniscate. Perhaps there is no need for an answer and one can imagine that the shape was the manifestation of Zumthor’s desire to create a space that encompasses the rituals of the Eucharist; renewing ancestral traditions of mass high up in the mountains above Sumvtig.Image 10: Google image -detail of the interior roof structure
Epilogue
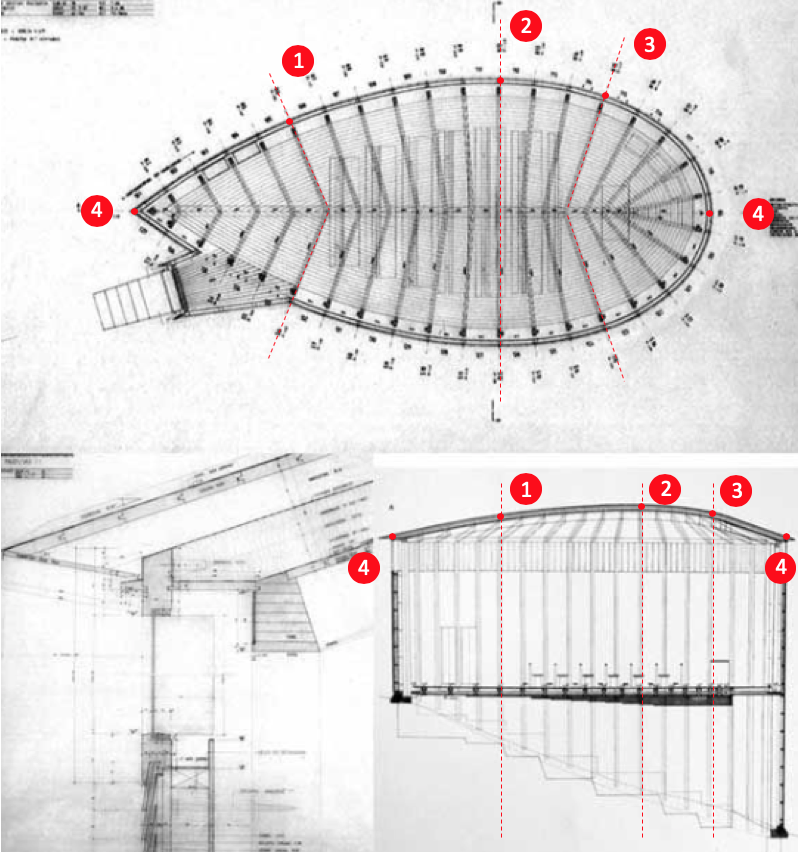
As a final note, and perhaps my epiphany in understanding the chapel as a three-dimensional artifact, is my discovery that the hump back shape of the roof is in direct correlation to the chapel’s plan. Great architecture always explores both plan and section, but rarely have I found a direct correspondence between the two. Why is this different and how did Zumthor accomplish this?
Image 11: Coordination between plan and section (author’s collection).
The elegance of Zumthor’s solution stems, perhaps, from a desire to “design” a roof and a ceiling that does not reflect an aesthetic choice, but respects the simplicity of the logic of the plan’s geometrical shape. To achieve this concept, Zumthor chose to maintain an identical pitch for each of the ceiling rafters throughout the chapel. In the illustration above demonstrates (Image 11, above), as the plan swells from point 4 to point 2 and back to 4 (from left to right), the roof takes on its shape as a result of the plan and the point of intersection of both rafters at point 1, 2, and 3. As described earlier, point 4 in plan and section correspond to the pole and the petal points of the lemniscate and become moments of zero elevation for the roof.
Often, simple architecture conceals the sophistication and complexity of the architect’s solution.
Architectural Education: Peter Zumthor Part 1 -the lemniscate